lineas de bezier

Se denomina curvas de Bézier a un sistema que se desarrolló hacia los años 1960 para el trazado de dibujos técnicos, en el diseño aeronáutico y en el de automóviles. Su denominación es en honor a Pierre Bézier, quien ideó un método de descripción matemática de las curvas que se comenzó a utilizar con éxito en los programas de CAD.

Las curvas de Bézier fueron publicadas por primera vez en 1962 por el ingeniero francés Pierre Bézier y posteriormente, trabajando en la Renault, las usó con abundancia en el diseño de las diferentes partes del automóvil. Las curvas fueron desarrolladas por Paul de Casteljau usando el algoritmo que lleva su nombre. Se trata de un método numéricamente estable para evaluar las curvas de Bézier.
Posteriormente, los inventores del PostScript, lenguaje que permitió el desarrollo de sistemas de impresión de alta calidad desde el ordenador, introdujeron en ese código el método de Bézier para la generación del código de las curvas y los trazados. El lenguaje PostScript sigue empleándose ampliamente y se ha convertido en un estándar de calidad universal; por ello, los programas de diseño vectorial como Adobe Illustrator, el extinto Macromedia FreeHand y Corel Draw, tres de los programas más importantes de dibujo vectorial y otros como Inkscape, denominan «bézier» a algunas de sus herramientas de dibujo, y se habla de «trazados bézier», «pluma bézier», «lápiz bézier», etc. Su facilidad de uso la ha estandarizado en el diseño gráfico, extendiéndose también a programas de animación vectorial, como Adobe Flash, y retoque fotográfico (bitmap), como Photoshop y Gimp, donde se usa para crear trazos, formas cerradas o selecciones.

Curvas lineales de Bézier

Dados los puntos P₀ y P₁, una curva lineal de Bézier es una línea recta entre los dos puntos. La curva viene dada por la expresión:

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+(\mathbf {P} _{1}-\mathbf {P} _{0})t=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\mbox{ , }}t\in [0,1].}$

Curvas cuadráticas de Bézier

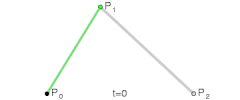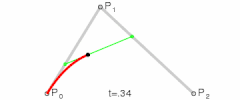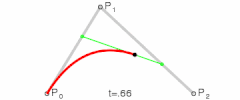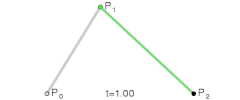
Una curva cuadrática de Bézier es el camino trazado por la función B(t), dados los puntos: P₀, P₁, y P₂,

${\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2t(1-t)\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}{\mbox{ , }}t\in [0,1].}$

Las fuentes de letras TrueType usan curvas de Bézier desdobladas compuestas por curvas cuadráticas de Bézier.

Curvas cúbicas de Bézier

Curva cúbica de Bézier donde se aprecian los puntos o nodos de anclaje P₁ y P₂.

Cuatro puntos del plano o del espacio tridimensional, P₀, P₁, P₂ y P₃ definen una curva cúbica de Bézier. La curva comienza en el punto P₀ y se dirige hacia P₁ y llega a P₃ viniendo de la dirección del punto P₂. Usualmente, no pasará ni por P₁ ni por P₂. Estos puntos solo están ahí para proporcionar información direccional. La distancia entre P₀ y P₁ determina "qué longitud" tiene la curva cuando se mueve hacia la dirección de P₂ antes de dirigirse hacia P₃.
La forma paramétrica de la curva es:

${\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}(1-t)^{3}+3\mathbf {P} _{1}t(1-t)^{2}+3\mathbf {P} _{2}t^{2}(1-t)+\mathbf {P} _{3}t^{3}{\mbox{ , }}t\in [0,1].}$

Los modernos sistemas de imágenes como PostScript, Asymptote y Metafont usan curvas de Bézier desdobladas, compuestas por curvas cúbicas de Bézier para dibujar las formas de las curvas.

Curvas lineales

La ${\displaystyle t}$ en la función para la curva lineal de Bézier se puede considerar como un descriptor de lo lejos que está ${\displaystyle B(t)}$ de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$. Por ejemplo cuando ${\displaystyle t=0.25}$, ${\displaystyle B(t)}$ es un cuarto de la longitud entre el punto ${\displaystyle P_{0}}$ y el punto ${\displaystyle P_{1}}$. Como ${\displaystyle t}$ varía entre 0 y 1, ${\displaystyle B(t)}$ describe una línea recta de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$.

Curvas cuadráticas

Para curvas cuadráticas se pueden construir puntos intermedios desde ${\displaystyle Q_{0}}$ a ${\displaystyle Q_{1}}$ tales que ${\displaystyle t}$ varía de 0 a 1: Punto ${\displaystyle Q_{0}}$ varía de ${\displaystyle P_{0}}$ a ${\displaystyle P_{1}}$ y describe una curva lineal de Bézier. Punto ${\displaystyle Q_{1}}$ varía de ${\displaystyle P_{1}}$ a ${\displaystyle P_{2}}$ y describe una curva lineal de Bézier. Punto ${\displaystyle B(t)}$ varía de ${\displaystyle Q_{0}}$ a ${\displaystyle Q_{1}}$ y describe una curva cuadrática de Bézier. Curvas de órdenes superiores Para curvas de orden superior se necesitan, lógicamente, más puntos intermedios. Para curvas cúbicas se pueden localizar puntos intermedios Q0, Q1 y Q2 que describen las curvas lineales de Bézier y los puntos R0 y R1 que describen las curvas cuadráticas: Y para curvas de grado 4, se pueden localizar los puntos intermedios Q0, Q1, Q2 y Q3 que describen las curvas lineales de Bézier, los puntos R0, R1 y R2 que describen las curvas cuadráticas y los puntos S0 y S1 que describen las curvas cúbicas.